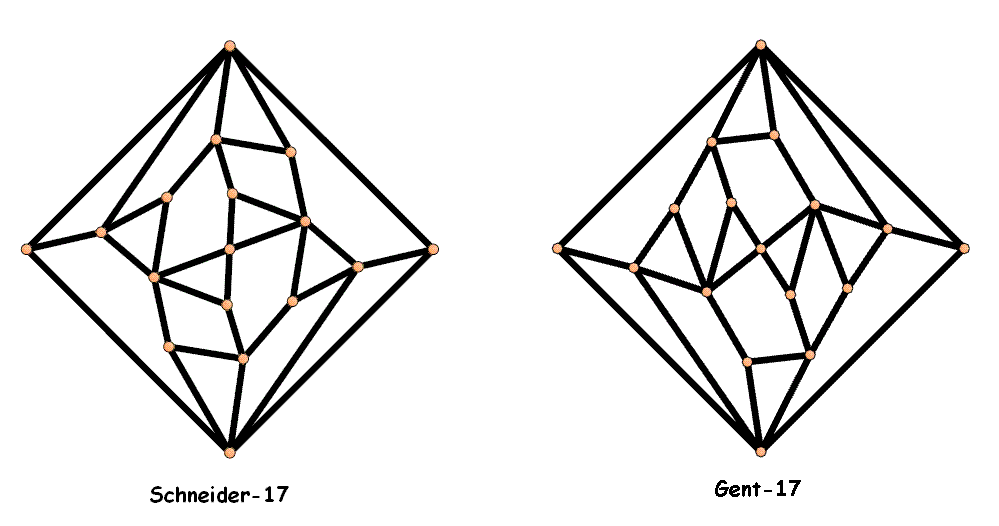Alternating Plane Graphs
Latest Update: December 01, 2014
Now a revised version of the paper on
"Alternating plane graphs" by
Jan Kristian Haugland, Karl Scherer, Frank Schneider,
Nicolas van Cleemput, and me exists and is under revision.
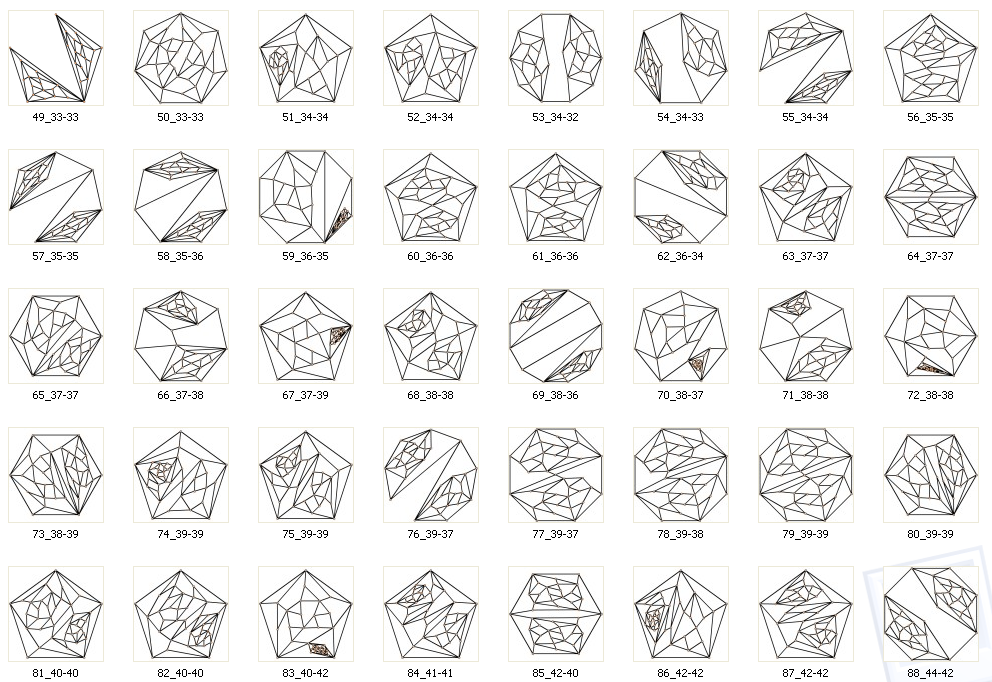
A central part of the paper is a description how alternating
plane graphs can be generated for all numbers of vertices
from 19 on. The proof is partly based on a list of explicitely
constructed alternating plane graphs. This table can be found
online at
this place
To get on idea of that list, look at the following two images.

The next three pictures show typical ways to merge apg's
to get larger ones.
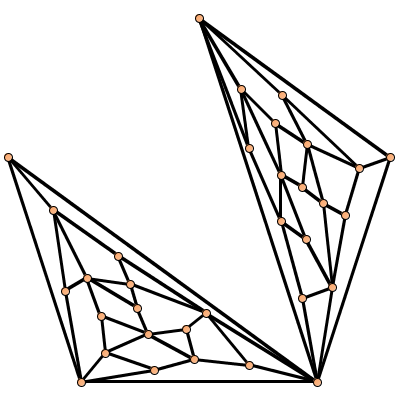
Glueing them together at a vertex

Glueing them together at a face

Embedding the second apg in a face of the first apg
*******************************************************************
Spring/Summer 2013
I designed a 2-player board game "Schneider von Gent" where either
the graph Schneider-17 or the Gent-17 are used as game board.
Click!

Frank Schneider found an alternating plane graph with
30 vertices, 33 faces, and 61 edges. This refutes a
conjecture of Karl Scherer, who thought that the difference
between number of vertices and faces coul differ by atmost 2.
Nicolas van Cleemput (Gent University) proved with computer help
that there
do not exist alternating plane graphs with 18 vertices.
A plane graph is called alternating, when the
following conditions are fulfilled:
* There are no neighbouring vertices with the same degree.
* There are no neighbouring faces with the same number
of sides. (Attention: the outer face of the graph is
also a face!)
* Each vertex has degree at least 3.
* Each face has at least 3 sides.
My motivation to introduce alternating plane graphs in 2008 came from
Karl Scherer's nice alternating tilings. Alternating
tilings are tilings with
several (at least two) types of tiles where no two tiles of the same
type touch each other. See for instance Karl's beautiful 20- and
21-solutions for squaring the square
here.
The 21-solution became the base for a variant of my game
EinStein würfelt nicht. Karl Scherer also has provided a nice
website on alternating plane graphs in the Wolfram Demonstrations
Project, click
here.
Back in 2008, I was in search of alternating plane graphs where
one of the following criteria is met:
* Number of vertices is very small -
or
* Number of vertices plus number of faces
is smaller than 34 (34 = 17 + 17 was from the record holder
Schneider-17, by Frank Schneider).
Record Holders
Feb 07, 2013: Gunnar Brinkmann and Nicolas van Cleemput
from Ghent
University found a second apg with 17 vertices and 17 faces.
Feb 06, 2008: Frank Schneider (Aachen): 17 vertices + 17 faces
Feb 02, 2008: Katrin Nimczick and Lisa Schreiber (Jena): 25
vertices + 25 faces
With massive computer help, the "Ghent group" proved that 17 is
the smallest number of vertices
for an alternating plane graph. On Feb 07, 2013, they announced
that there exist exactly
two non-isomorphic alternating plane graphs with 17 vertices:
the Schneider graph and another one which I call
Gent-17 in contrast to Schneider-17.
Both have 17 vertices and 17 faces.
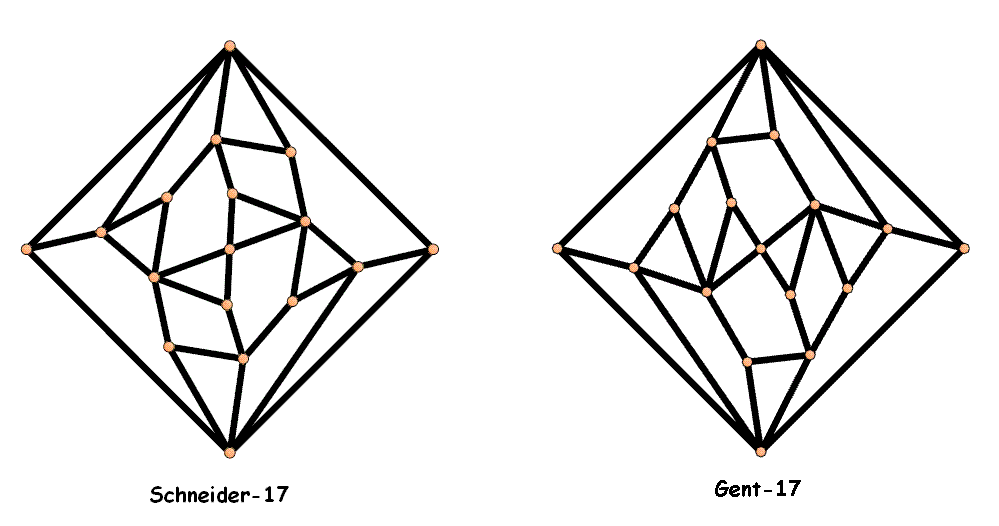


This 3-dimensional realisation of the Schneider graph was made with
the 3d-printer of the "Instrumental Analysis Group" of
"Ernst-Abbe-Fachhochschule" Jena.
Therefore, my thanks to the group, especially to the leader,
Prof. Dr. Karl-Heinz Feller,
and to his doctoral assistant Konrad Hoffmeier.
The 3d-coordinates had been optimized before by Frank Schneider himself.
Outside of Jena, the first person to touch the Schneider-17 was
Reinhold Wittig from Göttingen, wise guru ot the
German game designer scene.

Carefully, Reinhold took the valuable piece, turned it around several
times, and then mumbled: "Here is an axis of symmetry... no, just not ...
but now here, no, also not ... but here, no." Then he took up his head
and starred at me. "Reinhold", I started softly, "there are no axis
of symmetry in this body. This is fully intended."
The three pictures at the end of this page show the Schneider graph
in two different drawings (a very nice one by Jan Kristian Haugland
from Bergen/Norway; another one by Karl Scherer from New Zealand,
with the help of his program "Graph Puzzles" for
Zillions of Games)
and the Nimczick-Schreiber graph.
Observe that in the Schneider graph all degrees (for vertices and faces)
are from 3, 4, 5. Furthermore, this graph is self-dual. Jan Kristian
Haugland (alias "Tasmanian Devil" on LittleGolem) found
that in each alternating plane graph with the 3,4,5-restriction
the number of vertices and the number of faces are equal!
His proof may be found
here (somewhere in the middle of the lengthy thread).
For some time it was an open question whether each alternating plane
graph with (3,4,5)-restriction on the degrees is self-dual.
Frank Schneider gave a clear "No" by showing that several of "his"
(3,4,5)-apg's are not self-dual.
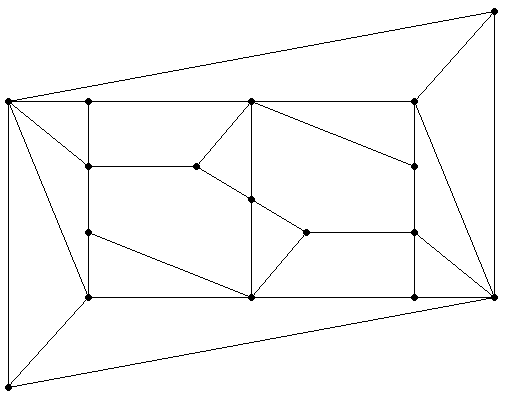
Frank Schneider: Alternating plane graph with 17 vertices
and 17 faces. Graph drawing by Jan Kristian Haugland.

Frank Schneider: 3-dimensional paper realisation
of his graph. We intend to make a 3d-version
with solid material.
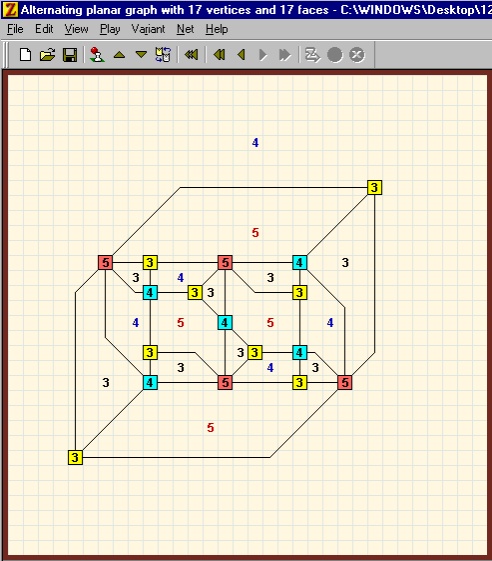
Frank Schneider: Alternating plane graph with 17 vertices and 17 faces
Graph drawing by Karl Scherer with help of his program "Graph Puzzles"
for "Zillions of Games".
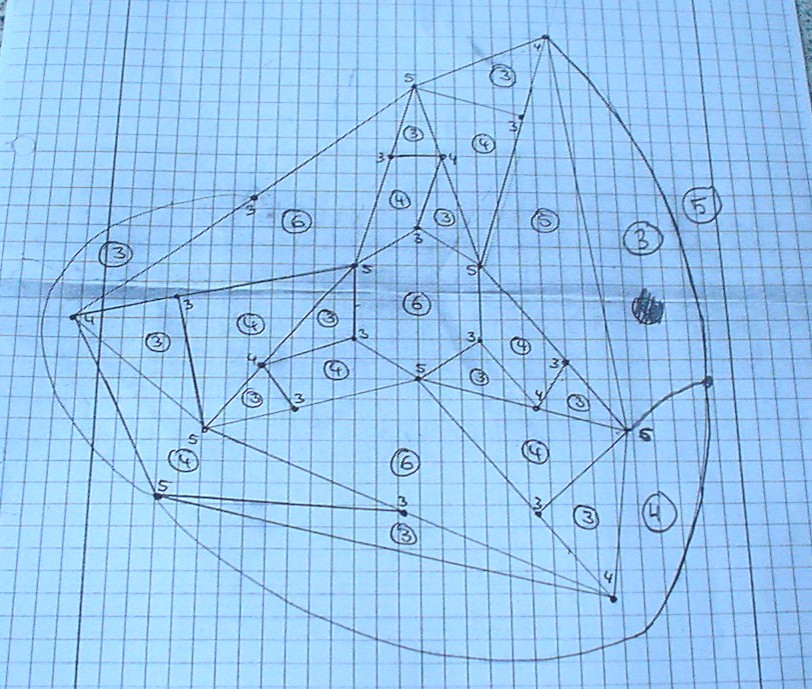
K. Nimczick and L. Schreiber: the very first apg (with 25 vertices
and 25 inner faces)
New Contributions are welcome to the email address mentioned
on the main site.
My interest in alternating plane graphs comes from
work of Karl Scherer on alternating tilings of
a square by smaller squares.
Back to the main site of Ingo Althofer